Chapitre 4 : Modéliser
Qui dit Machine Learning dit algorithme entraîné à partir de données afin de prédire un résultat sur un nouveau jeu de données. Cette branche de l’intelligence artificielle se différencie de l’économétrie notamment à travers leurs objectifs : si l’économétrie s’attache à comprendre les phénomènes en s’appuyant sur des modèles explicatifs et recherchant à évaluer la causalité de x sur y, le Machine Learning se focalise sur un simple objectif prédictif en exploitant les relations de corrélations entre les variables.
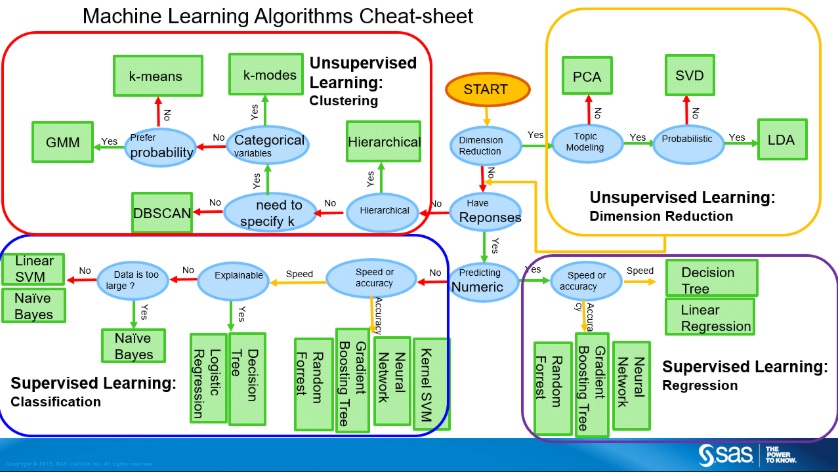
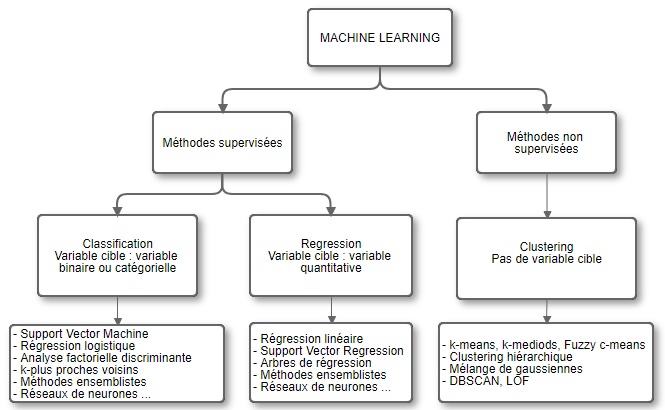
Voici un schéma usuel qui donne un premier aperçu des différentes méthodes de Machine Learning :
Mais comment choisir entre les modèles ?
Ce tutoriel vise à expérimenter l’implémentation de quelques méthodes de Machine Learning en python sans founir les explications théoriques de ces méthodes. Toutefois, même s’il ne dispense pas de comprendre les différentes méthodes, on peut quand même s’appuyer sur ce schéma simplifié pour orienter nos choix de modèle :
On peut aussi s’appuyer sur le cheatsheet de scikit-learn. Enfin, afin de comprendre le fonctionnement intuitif de chaque méthode, il peut être utile de consulter un cours de Machine Learning.
Le site Machine Learning Mastery propose des explications intuitives sur les principales méthodes de Machine Learning. Le livre Introduction to Machine Learning with Python fournit quelques explications sur de nombreux algorithmes et précise le code python nécessaire pour les mettre en oeuvre.
I) Commencer par prédire une variable catégorielle binaire : un problème de classification
Pour réaliser ce tutoriel, on a enrichi les données précédentes avec des données socio-démographiques. On met donc à disposition une base, nommée tableModelisation, contenant les villes de plus de 20 000 habitants. Une indicatrice, nommée plus50, constituée à partir de la présence de l’absence de la ville dans la table de l’isf manipulée précédemment, indique si plus de 50 redevables paient l’isf dans la ville. Vous pouvez consulter le dictionnaire des données qui s’appelle Dictionnaire_tableModelisation.
La modélisation sera réalisée à partir des prédicteurs socio-démographiques suivants :
- la proportion de résidences principales de type maison (P15_RPMAISON),
- la proportion de résidences principales de moins de 30 m² (P15_RP_M30M2),
- la proportion de résidences principales de 30 à moins de 60 m² (P15_RP_3060M2),
- la proportion de résidences principales de 80 à moins de 100 m² (P15_RP_80100M2),
- la proportion de résidences principales de 100 m² ou plus (P15_RP_100M2P),
- la proportion de familles monoparentales (C15_FAMMONO),
- la proportion de familles formées d’un couple sans enfant (C15_COUPSENF),
- la proportion de personnes non scolarisées de 15 ans ou plus titulaires d’aucun diplôme ou au plus un BEPC, brevet des collèges ou DNB (P15_NSCOL15P_DIPLMIN),
- la proportion de personnes non scolarisées de 15 ans ou plus titulaires d’un CAP ou d’un BEP (P15_NSCOL15P_CAPBEP),
- la proportion de personnes non scolarisées de 15 ans ou plus titulaires d’un diplôme de l’enseignement supérieur (P15_NSCOL15P_SUP).
1) Préparer ses données
Exercice 1 : Vérifier qu’il n’y a pas de valeurs manquantes dans la base de données
# On commence par charger les donnnées.
import pandas as pd
tableModelisation=pd.read_csv("tableModelisation.csv")
# Solution 1 :
tableModelisation[np.any(tableMod[['plus50','P15_NSCOL15P_DIPLMIN', 'P15_NSCOL15P_CAPBEP', 'P15_NSCOL15P_SUP',
'C15_FAMMONO', 'C15_COUPSENF',
'P15_RPMAISON', 'P15_RP_M30M2', 'P15_RP_3060M2', 'P15_RP_80100M2', 'P15_RP_100M2P']].isna().values, axis=1)]
# Solution 2 :
np.any(tableModelisation[['plus50','P15_NSCOL15P_DIPLMIN', 'P15_NSCOL15P_CAPBEP', 'P15_NSCOL15P_SUP',
'C15_FAMMONO', 'C15_COUPSENF',
'P15_RPMAISON', 'P15_RP_M30M2', 'P15_RP_3060M2', 'P15_RP_80100M2', 'P15_RP_100M2P']].isna())
Exercice 2 : Observer la répartition de chaque variable
from pandas.plotting import scatter_matrix
scatter_matrix=scatter_matrix(tableModelisation[['plus50','P15_NSCOL15P_DIPLMIN', 'P15_NSCOL15P_CAPBEP', 'P15_NSCOL15P_SUP',
'C15_FAMMONO', 'C15_COUPSENF',
'P15_RPMAISON', 'P15_RP_M30M2', 'P15_RP_3060M2', 'P15_RP_80100M2', 'P15_RP_100M2P']], alpha=0.9, figsize=(9, 9), diagonal='hist')
for ax in scatter_matrix.ravel():
ax.set_xlabel(ax.get_xlabel(), fontsize = 6, rotation = 90)
ax.set_ylabel(ax.get_ylabel(), fontsize = 6, rotation = 0)
plt.tight_layout(pad=0.01)
Exercice 3 : Séparer les données entre échantillon d’apprentissage et échantillon de test. Pourquoi est-ce utile ?
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(tableModelisation[['P15_NSCOL15P_DIPLMIN', 'P15_NSCOL15P_CAPBEP',
'P15_NSCOL15P_SUP', 'C15_FAMMONO', 'C15_COUPSENF', 'P15_RPMAISON', 'P15_RP_M30M2', 'P15_RP_3060M2',
'P15_RP_80100M2', 'P15_RP_100M2P']], tableModelisation['plus50'], test_size=0.33, random_state=42)
L’utilisation d’un échantillon d’apprentissage et d’un échantillon de test permet de réduire les risques de sur-apprentissage (overfitting), c’est-à-dire d’opter pour un modèle qui colle trop parfaitement aux données. Ainsi, choisir son modèle, estimé à partir de l’échantillon d’apprentissage, en l’évaluant sur un échantillon de test permet de se prémunir contre ce risque.
Afin de construire un modèle pertinent, la varaible à prédire doit être bien représentée dans les deux échantillons. Plus particulièrement, lorsqu’une modalité de la variable à prédire est rare, il faut s’assurer qu’elle soit présente dans les échantillons d’apprentissage et de test.
Par ailleurs, selon la même logique, il peut être utile de se constituer un échantillon de validation si on dispose de paramètres à ajuster.
Toutefois, comme nous venons de l’évoquer la séparation entre échantillon d’apprentissage sur lequel on estime le modèle et échantillon de test sur lequel on évalue le modèle est indispensable afin d’éviter le sur-apprentissage mais elle implique mécaniquement un entraîenement du modèle sur un jeu de données restreint avec un risque de biais par entraînement du modèle sur un jeu de données potentiellement spécifique et non représentatif de la population complète. Cette séparation est d’autant plus problématique lorsque le jeu de données est petit. La validation croisée peut permettre de satisfaire la contrainte de séparation entre apprentissage et évaluation et l’ambition de ne pas se restreindre par hasard à une population spécifique. Cela consiste à découper le jeu de données en k sous ensembles et à utiliser respectivement ces k sous-ensembles comme échantillon de test alors que les k-1 restantes sont utisées pour entraîner le modèle. Dans le cadre de la validation croisée, la performance globale du modèle est évaluée soit en utilisant l’ensemble des prédictions sur le jeu de données complet réalisées sur les échantillons de test respectifs au cours de la procédure, soit en effectuant une moyenne des performances des modèles sur les k échantillons de test.
Exercice 4 : Les trois variables issues de la table sur l’isf (le nombre de redevables, le patrimoine moyen et l’impôt moyen) sont manquantes pour les villes où ce nombre est inférieur à 50. Si ces valeurs manquantes étaient aléatoires, comment auriez-vous pu les imputer ?
Scikit-learn offre plusieurs stratégies d’imputation présentées globalement sur leur site sous ce lien ou sous ce lien qui présente les options de la fonction SimpleImputer.
Si les valeurs manquantes relatives aux trois variables résultaient d’un processus aléatoire, et non issues du fait qu’il manquait car le nombre de redevables était inférieur à 50, alors on pourrait imputer les valeurs manquantes à leur moyenne avec le code ci-dessous par exemple :
from sklearn.impute import SimpleImputer
imp_mean = SimpleImputer(missing_values=np.nan, strategy='mean')
donnees_imputees=pd.DataFrame(imp_mean.fit_transform(tableModelisation[['nombre de redevables', 'patrimoine moyen en €', 'impôt moyen en €']]), columns=['nombre de redevables', 'patrimoine moyen en €', 'impôt moyen en €'])
donnees_imputees.head(2)
On pourrait aussi envisager d’utiliser la fonction fillna de pandas. Une autre solution serait de construire un modèle de prédiction pour chaque variable contenant des valeurs manquantes et de remplacer les valeurs manquantes par la valeur prédite.
Exercice 5 : Pourquoi est-il préférable, voire impératif, de redimensionner (normaliser et/ou standardiser) les données ?
Plusieurs raisons peuvent justifier le redimensionnement des données (feature scaling) :
-
le feature scaling permet d’éviter les problèmes d’échelles, notamment problématiques lors du calcul de distance entre deux points. Par exemple, si une variable comprend des données très dipersées tandis que les autres prennent des valeurs comprises entre 0 et 1, ces dernières valeurs risquent d’être non significatives dans le calcul de la distance euclidienne. L’algorithme est alors seulement influencé par la première dimension.
-
le feature scaling favorise la convergence lors de la descente de gradient. Une trop grande différence d’ordre de grandeur entre les variables perturbe la convergence du modèle, comme l’indique notamment cet article. Plus précisément, pour les algorithmes qui reposent sur une minimisation d’une fonction de coût par descente de gradient, conserver des données avec des ordres de grandeurs très différents entraîne des différences de vitesses de convergence des paramètres. Dans ce cas, la minimisation de la fonction de coût est plus lente et la descente de gradient met donc plus de temps à trouver le modèle optimal.
Par exemple, le feature scaling s’avère indispensable dans les cas suivants :
- lorsque des paramètres sont calculés à partir d’une descente de gradient, comme dans le cas de la régression linéaire, la régression polynomiale, la régression logistique …
- lorsque le degré de similarité entre deux observations s’appuie sur un calcul de distance comme dans le cas des k-plus-proches voisins
- avec des méthodes de clustering comme le kmeans
Exercice 6 : Citez deux grandes méthodes de redimensionnement et mettez les en oeuvre
- La standardisation consiste à centrer et réduire les données. En théorie, les variables suivent une distribution normale avec des moyennes et des écart-types différents puis suite à la standardisation, elles suivent une loi normale centrée réduite. En pratique,la distribution des variables est généralement inconnue.
from sklearn import preprocessing
scaler = preprocessing.StandardScaler().fit(X_train)
X_train_standardise=scaler.transform(X_train)
# On s'assure que les données sont bien de même dimension
print(X_train.shape)
print(X_train_standardise.shape)
# On applique la standardisation à l'échantillon de test
X_test_standardise=scaler.transform(X_test)
- La normalisation min-max consiste à restreindre l’intervalle des données à [0,1] par la formule suivante :
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler().fit(X_train)
X_train_minmax = min_max_scaler.transform(X_train)
# On s'assure que les données sont bien de même dimension
print(X_train.shape)
print(X_train_minmax.shape)
# On applique le min-max à l'échantillon de test
X_test_minmax=scaler.transform(X_test)
D’autres méthodes de normalisation des données sont implémentées dans scikit-learn, vous pouvez les consulter sur leur site.
2) Choisir et tester différentes méthodes
Avec la standardisation, vous venez de vous découvrir la logique d’implémentation de scikit-learn. Détaillons la structure du code pour implémenter un algorithme de Machine Learning avec scikit-learn :
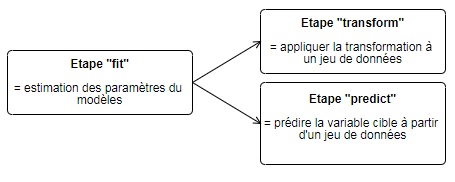
Le transform permet d’appliquer une transformation à un jeu de données pour modifier ces dernières. Pour la standardidation, la fonction fit estime la moyenne et l’écart-type sur un jeu de données, ici l’échantillon d’apprentissage, puis la fonction transform centre et réduit les données indiquées en paramètre (soit l’échantillon d’apprentissage, soit l’échantillon de test dans notre exemple). Notons qu’il est possible d’effectuer les étapes d’estimation (fit) et de transformation du jeu de données (transform) en une seule étape grâce à a fonction fit_transform.
Le predict prédit la valeur de la variable cible. Par exemple, avec le modèle de régression logistique, le predict estimera à partir du modèle pré-entrainé avec le fit, les labels associés au jeu de données, dans notre cas à l’échantillon de test.
Exercice 7 : Appliquer une régression logistique
N’hésitez pas à consulter l’aide détaillée de scikit-learn relative à la régression logitique.
from sklearn.linear_model import LogisticRegression
clf_logistic = LogisticRegression(solver='liblinear')
clf_logistic.fit(X_train_standardise, np.array(y_train))
y_test_logistic_predit = clf_logistic.predict(X_test_standardise)
print(y_test_logistic_predit.shape)
Exercice 8 : Puis appliquer un Support Vector Machine (SVM) ?
| Un petit zoom sur les SVM |
|---|
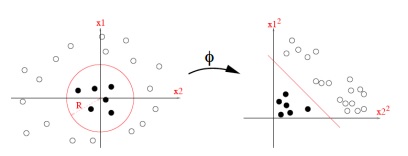
| Les Vector Support machine (SVM) visent à séparer linéairement les observations dans un espace de très grande dimension. Selon le principe schématisé sur la Figure ci-dessous, cet espace de grande dimension résulte de la transformation ϕ, potentiellement non linéaire, de l’espace des variables d’origine. Une transformation non linéaire, réalisée via une fonction noyau ϕ, peut ainsi favoriser la séparation linéaire des observations dans le nouvel espace.
|
from sklearn import svm
clf_svm = svm.kernel='linear', probability=True)
clf_svm.fit(X_train_standardise, y_train)
L’option probability=True permet d’obtenir par la suite les probabilités d’appartenance à chaque label. Le paramètre étant par défaut mis à False, les probabilités ne sont alors pas disponibles lors de la prédiction et la courbe ROC, présentée ci-dessous, ne peut pas être évaluée et représentée.
y_test_svm_predit = clf_svm.predict(X_test_standardise)
print(y_test_svm_predit.shape)
Exercice 9 : Même si on ne peut pas interpréter le pouvoir explicatif d’une variable sur la variable cible, on peut toutefois s’intéresser à l’importance de chaque variable dans le modèle de prédiction. Représenter les coefficients par ordre décroissant.
coef = clf_svm.coef_[0]
nb_features=len(coef)
feature_names=['P15_NSCOL15P_DIPLMIN', 'P15_NSCOL15P_CAPBEP', 'P15_NSCOL15P_SUP', 'C15_FAMMONO', 'C15_COUPSENF', 'P15_RPMAISON', 'P15_RP_M30M2', 'P15_RP_3060M2', 'P15_RP_80100M2', 'P15_RP_100M2P']
top_coefficients = list(np.argsort(coef))
# Représentation graphique des résultats
plt.figure(figsize=(20, 8))
colors = ['red' if c < 0 else 'blue' for c in coef[top_coefficients]]
plt.barh(np.arange(nb_features), coef[top_coefficients], color=colors, height=0.8)
feature_names = np.array(feature_names)
plt.yticks(np.arange(nb_features), feature_names[top_coefficients], rotation=0, ha='right')
plt.show()
Ce code s’applique seulement au SVM avec un noyau linéaire. Par exemple, pour une partie des méthodes, comme les forêts aléatoires, une variable importance est directement disponible dans scikit-learn. Vous pouvez trouver quasi systématiquement sur internet le code nécessaire pour observer et représenter l’importance des prédicteurs.
3) Evaluer et comparer les performances des algorithmes
La précision et le rappel (recall en anglais) constituent deux critères qui mettent en exergue les capacités d’un classifieur. Ils sont notamment pertinents dans le cas où les classes sont déséquilibrées.
La précision analyse la qualité du prédicteur pour les observations détectées comme positives par le modèle. Pour nos modèles, la précision correspond donc au nombre de villes où plus de 50 personnes sont réellement redevables et qui sont détectés par le modèle rapporté au nombre total de villes détectées par le modèle (à tort et à raison) comme habritant plus de 50 redevables de l’isf. Elle se déduit de la formule suivante :
$$ \text{Précision } = \frac{\text{Nombre de vrais positifs}}{\text{Nombre de vrais positifs } + \text{ Nombre de faux positifs}} $$
De façon complémentaire, le rappel, aussi appelé la sensibilité, se focalise sur la qualité du modèle pour la classification des observations positives. Dans notre exemple, le rappel désigne la part des villes comme ayant plus de 50 redevables en réalité et selon le modèle par rapport à l’ensemble des villes où plus de 50 personnes sont réellement redevables. Le rappel se calcule donc selon la formule suivante :
$$ \text{Rappel }=\frac{\text{Nombre de vrais positifs}}{\text{Nombre de vrais positifs } + \text{ Nombre de faux négatifs}} $$
Une troisième notion, complémentaire à la sensibilité, peut être utilisée. Si la sensibilité s’intéresse aux observations avec un label effectif positif, la spécificité étudie les observations avec un label effectif nul. Parmi ces derniers, c’est-à-dire parmi les villes où moins de 50 personnes sont réellement redevables par exemple, la spécificité étudie la probabilité d’être aussi considérées comme tel par le modèle de prédiction.
$$ \text{Spécificité }=\frac{\text{Nombre de vrais négatifs}}{\text{Nombre de vrais négatifs } + \text{ Nombre de faux positifs}} $$
Exercice 9 : Evaluer les performances des deux modèles en affichant leur matrice de confusion
On peut utiliser la fonction fournissant la matrice de confusion brute qui est détaillée dans ce lien. Afin d’obtenir un résultat plus visuel, on peut reprendre la fonction proposée sur le site de scikit-learn pour mettre en forme cette matrice. Le code de cette fonction est présentée ci-dessous :
from sklearn.metrics import confusion_matrix
from sklearn.utils.multiclass import unique_labels
def plot_confusion_matrix(y_true, y_pred, classes,
normalize=False,
title=None,
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if not title:
if normalize:
title = 'Normalized confusion matrix'
else:
title = 'Confusion matrix, without normalization'
# Compute confusion matrix
cm = confusion_matrix(y_true, y_pred)
# Only use the labels that appear in the data
classes = classes[unique_labels(y_true, y_pred)]
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
fig, ax = plt.subplots()
im = ax.imshow(cm, interpolation='nearest', cmap=cmap)
ax.figure.colorbar(im, ax=ax)
# We want to show all ticks...
ax.set(xticks=np.arange(cm.shape[1]),
yticks=np.arange(cm.shape[0]),
# ... and label them with the respective list entries
xticklabels=classes, yticklabels=classes,
title=title,
ylabel='True label',
xlabel='Predicted label')
# Rotate the tick labels and set their alignment.
plt.setp(ax.get_xticklabels(), rotation=45, ha="right",
rotation_mode="anchor")
# Loop over data dimensions and create text annotations.
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(j, i, format(cm[i, j], fmt),
ha="center", va="center",
color="white" if cm[i, j] > thresh else "black")
fig.tight_layout()
return ax
On applique cette fonction pour obtenir la matrice de confusion dans le cas de la régression logistique :
plot_confusion_matrix(y_test, y_test_logistic_predit, classes=np.unique(y_test),
title='Confusion matrix, without normalization')
On l’applique ensuite au cas du SVM :
plot_confusion_matrix(y_test, y_test_svm_predit, classes=np.unique(y_test),
title='Confusion matrix, without normalization')
Dans le cadre d’une classification binaire, la courbe ROC et l’aire sous la courbe associée (Area Under the Cruve - AUC) fournissent une information plus précise de la qualité du modèle que le simple taux d’erreur ou que la matrice de confusion. En effet, ces critères utilisent un seuil fixe, par défaut 0,5, selon lequel l’observation est classée ou non dans la catégorie des villes où plus de 50 personnes sont redevables de l’isf par exemple. A l’inverse, la courbe ROC représente la proportion de vrais positifs, par exemple des villes où plus de 50 personnes sont réellement redevables de l’isf et détectées à raison par le modèle, selon la proportion de faux positifs, c’est-à-dire les villes où moins de 50 personnes sont redevables de l’isf mais où le modèle détecte l’inverse. Comme nous souhaitons minimiser le risque de première espèce qui correspond au taux de faux positifs tout en maximisant la puissance du test égal au taux de vrais positifs, la courbe ROC idéale augmente très rapidement vers 1 puis est égale à 1 pour tous les taux de vrais positifs différents de 0 (\og coude \fg{}). Cette situation indique que, pour un seuil donné, le modèle ne commet pas d’erreur.
L’AUC mesure la performance du modèle par rapport à cette situation idéale. Ainsi, plus l’AUC est grand, meilleur est le modèle. En effet, une AUC élevée indique que lorsque le seuil de décision diminue, le modèle détecte plus rapidement une proportion forte de villes où plus de 50 personnes sont redevables de l’isf et une faible proportion de villes où moins de 50 personnes sont redevables de l’isf.
Exercice 11 : Comparer les deux modèles, notamment à l’aide de leurs courbes ROC
# On commence par prédire non plus le label mais la probabilité d'appartenance à un label
from sklearn.metrics import roc_curve, auc
probas_logistic = clf_logistic.predict_proba(X_test_standardise)
probas_svm = clf_svm.predict_proba(X_test_standardise)
# Valeurs de la courbe ROC pour la régression logistique et le SVM
from sklearn import metrics
fpr_logistic, tpr_logistic, thresholds_logistic = metrics.roc_curve(y_test, np.transpose(probas_logistic)[1])
fpr_svm, tpr_svm, thresholds_svm = metrics.roc_curve(y_test, np.transpose(probas_svm)[1])
# Valeurs des aires sous la courbe
roc_auc_logistic = auc(fpr_logistic, tpr_logistic)
roc_auc_svm = auc(fpr_svm, tpr_svm)
%matplotlib inline
plt.figure(figsize=(9,7))
lw = 1.5
plt.plot(fpr_logistic, tpr_logistic, color='magenta',
lw=lw, label='Pour la régression logistique (area = %0.2f)' % roc_auc_logistic)
plt.plot(fpr_svm, tpr_svm, color='darkorange',
lw=lw, label='Pour un SVM (area = %0.2f)' % roc_auc_svm)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Taux de faux positifs')
plt.ylabel('Taux de vrais positifs')
plt.title('Courbes ROC des deux classifications')
plt.legend(loc="lower right")
plt.show()
Pour réaliser ces premières prédictions, on s’est contenté de prédicteurs socio-démographiques. Aucune variable précisant la localisation géographique a été introduite, ignorant alors l’existence d’autocorrélation spatiale, pourtant suggérée par la littérature sur la ségrégation spatiale. Cette omission (certes volontaire) n’introduit pas de biais environnemental comme cela serait le cas dans le cadre d’un modèle explicatif mais elle peut réduire le pouvoir prédictif de notre modèle.
Exercice 12 : Même si dans notre cas, l’apport de la localisation géographique n’est pas forcément facilement démontrable car la base de données est restreinte en raison du ciblage des villes de plus de 20000 habitants et par conséquent l’échantillon de test est de petite dimension avec de nombreux espaces géographiques non présents, représenter la carte des résidus par département.
# Comme précisé dans le chapitre sur la manipulation de données géographiques, on commence par installer les packages nécessaires.
!pip install geopandas mapclassify descartes pysal
# On importe aussi le fond de cartes départemental et on le charge dans une table dep.
import zipfile
with zipfile.ZipFile('dep_francemetro_2018.zip', 'r') as zip_ref:
zip_ref.extractall()
import geopandas as gpd
dep = gpd.read_file('dep_francemetro_2018.shp')
# On reconstitue la base restreinte à l'échantillon de test contenant l'erreur de prédiction
ech_test=tableModelisation.loc[list(X_test.index),:]
ech_test['y_test_logistic_predit']=y_test_logistic_predit
ech_test['erreur']=np.abs(ech_test['plus50']-ech_test['y_test_logistic_predit'])
# On agrège les données par département. Etant donné le souhait de mettre en évidence les départements où une erreur de prédiction a été commise, on choisit de considérer le département en erreur dès qu'une erreur a été commise pour une commune au sein du département.
ech_test_parDep=ech_test.groupby('dep', as_index=False)['erreur'].max()
# On fusionne les données avec le fond de cartes.
cartes = pd.merge(dep, ech_test_parDep, left_on = "code", right_on="dep", how="right")
# On représente ensuite les erreurs par département.
cartes.plot('erreur', legend=True, categorical=True, figsize=(8, 8))
On constate une légère corrélation spatiale des erreurs suggérant l’intérêt d’introduire une variable géographique. Attention, dans notre exemple, en raison du choix de la problématique, nos données sont très restreintes et les résultats de cette analyse sont potentiellement sur-interprétés. Cette question met surtout l’accent sur l’importance d’observer les résidus, et notamment géographiquement, afin de vérifier que des prédicteurs pertinents n’ont pas été omis.
Vous pouvez alors refaire les modèles en introduisant la variable de département. Attention, celle-ci n’est pas une variable quantitative ordonnée, il faut donc la discrétiser. Le risque est d’introduire un très grand nombre d’indicatrices. Peut-être est-il alors pertinent de régulariser le modèle.
Besoin d’un résumé du processus avant de passer à la régression ?
II) Expérimenter la prédiction d’une variable quantitative : un problème de régression
On va maintenant se restreindre aux villes de plus de 20 000 habitants dans lesquelles plus de 50 personnes sont redevables de l’isf. Cela revient donc à se restreindre aux champs de la base isf manipulée dans les tutoriels précédents. On testera ici simplement un modèle de régression linéaire mais vous pouvez évidemment tester d’autres méthodes de régression si vous avez le temps !
Exercice 13 : Evaluer un modèle de régression pour prédire le nombre de redevables dans cette base restreinte puis prédire ce nombre sur un échantillon de test.
Vous pourriez réappliquer le code de la partie précédente en vous référant à la documentation scikit-learn sur la régression linéaire.
Il est aussi possible d’inclure les différentes étapes jusqu’à la prédiction au sein d’une seule chaîne de traitement, dite pipeline. Pour la mettre en place, vous pouvez consulter la documentation sur les pipelines dans scikit-learn.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(plus50[['P15_NSCOL15P_DIPLMIN', 'P15_NSCOL15P_CAPBEP', 'P15_NSCOL15P_SUP', 'C15_FAMMONO', 'C15_COUPSENF', 'P15_RPMAISON', 'P15_RP_M30M2', 'P15_RP_3060M2', 'P15_RP_80100M2', 'P15_RP_100M2P']], plus50['nombre de redevables'], test_size=0.33, random_state=42)
from sklearn.pipeline import Pipeline
scaler = preprocessing.StandardScaler()
reg = LinearRegression()
pipe = Pipeline(steps=[('scaler', scaler), ('reg', reg)])
reg_standard=pipe.fit(X_train, y_train)
# On évalue le R² du modèle
reg_standard.score(X_test, y_test)